The Concise Oxford Dictionary defines mathematics as “the abstract study of number, quantity, and space”. Skemp (1971) observed that having a concept entails more than just knowing its name; it also entails being able to apply the insight gained by seeing similarities across different examples of the concept.
Children create concepts as a result of events and reasoning about those experiences, according to Freudenthal (1973). This may seem far away to children from birth to eight, but infants and young children are naturally curious and begin to explore their surroundings at a young age. They don’t divide their investigations into mathematical and non-mathematical categories. They will, nevertheless, come across mathematical concepts such as number, amount, and shape.
Read More: Math Phobia: Causes, Symptoms, Ways to Overcome
Mathematics is an important area of learning and information for both adults and children in their daily lives. It offers children a uniquely powerful set of tools to comprehend and transform the world, according to the National Curriculum. Logical reasoning, problem-solving skills, and the ability to think abstractly are among these tools. It gives us the ability to govern and direct numerous parts of our existence. It is also a creative discipline that may be employed in various ways to communicate precisely. It can also be viewed as a continuous refinement and development of a web of concepts. Place value and the number system, conservation of numbers and measures, equivalence relations and dimensionality, and similarity relations are some of the; ’major notions’ of mathematics for young children.
“Children must Grasp Certain Logical Principles to understand Mathematics” – Piaget
However, some children lose interest in math by the middle of elementary school. Although there are several reasons for students’ apathy and irritation, the most obvious is that they are having difficulty acquiring mathematical concepts. Their incapacity to learn is caused by two factors, a failure of proper academic instructions, and specific cognitive deficits in children.
Read More: How to help kids Overcome Math Anxiety
Math Proficiency
The components of Math Proficiency, the overall goal of Modules for Math, are depicted in Figure 1. It depicts the well-known breakdown of Math Proficiency into computational and word problems. Computing’s primary cognitive process is planning/executive functioning (EF) whereas simultaneous processing is essential for understanding word problems. Attentional control (Geary, 2013) is included in Planning/EF. Similarly, logical-grammatical relationships (following Luria, in PASS theory) are included in simultaneous processing. The last level emphasises EF’s two components, inhibition, and shifting. Nonverbal (matrices-type tests) and verbal–simultaneous examinations are used to assess logical and grammatical divisions in word problems.

“If Mathematical Problem-Solving is always used in the Classroom…The Social Definition of Mathematics Become the use of School – Taught routines.” – Nunes & Bryant
5 Modules in Mathematics Children Must Learn
- Shifting Patterns to learn size and value
- Learning about Number Line
- Let us Count to learn numerosity
- Mapping, Meaning, and Estimating covering Verbal and Non-Verbal Simultaneous
- Memory Span for Numbers to keep working memory intact
Math Skills Children Learn in Beginning Math
The most frequently mentioned five skills in current literature and academia that target and seek to improve different mathematical skills are
- Size and Value
- Number Line
- Numerosity (Counting)
- Verbal and Non-Verbal Simultaneous
- Working Memory
Attentional Control
Planning/EF appears to be the most significant, if not the only, requirement for learning math, according to research. The role of EF is summarized by Geary (2013) as ‘Attentional Control’ and explains that children who possess the capacity to sustain attentional control and focus, as well as the capacity to suppress unwanted internal and external distractions, learn and remember target information in mind while processing other information, and it can be measured by working memory.
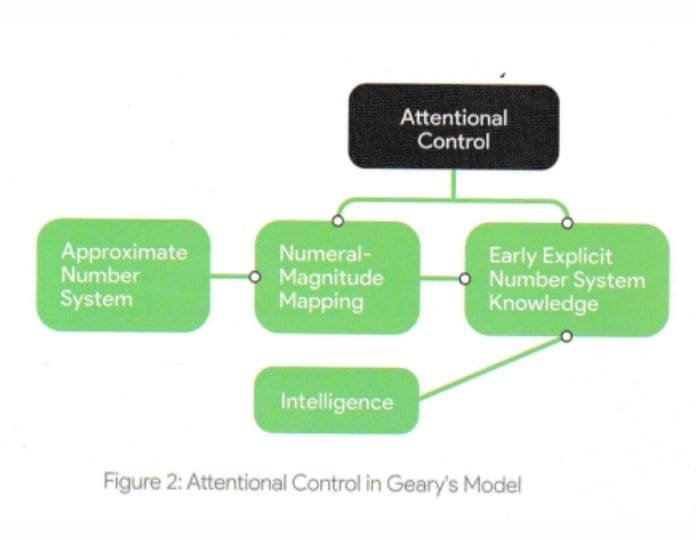
‘Attentional control,’ according to Geary’s model, is the primary cognitive process that drives all other processing. As per PASS theory, it is essentially similar to planning rather than attention. Attentional control, numeral-magnitude mapping, early explicit number system knowledge, approximate number system knowledge, and intelligence are the four cognitive factors active at the beginning of children’s mathematical learning, according to his model.
Approximate Number System
An individual’s intuitive awareness of a collection of items is the first step toward acquiring mathematics. In comparison to one toy, a baby’s sight is drawn to a larger group of toys (excluding favouritism). Number words (one, two, three) and Arabic numerals are the first abstract mathematical symbols that children learn (0 to 9). When these symbols are mapped into a numerical sense, they gain meaning. An entire training module has been dedicated to the approximate number system because it’s so crucial.
Explicit Number System
Number words and Arabic numerals are the first abstract mathematical symbols that children learn, and they gain significance when they are mapped onto this number sense. The next crucial stage is to have a clear knowledge of the relationships between numerals.
Patterns Shifting – W and M Test
The ability to shift is one of the three components of Executive Functioning (or planning). This ability is tested in the following tasks (Parts A, B, and C), which require the participant to add, subtract, multiply, or divide according to the activity and the letter “W” or “M” displayed. Except for Part C, each assignment has three practice sets and eight test questions that include both “W” and “M” patterns. Furthermore, the assignments demand that students not only recognize the shape of the two letters mentioned, but also apply the rule (to be taught), switch between addition and subtraction, multiplication and division, and perform simple math.
As per the example shown below, in the first activity, students will be required to add one when given the letter “W” and subtract one when given the letter “M”. The second exercise is identical to the first, with the exception that the learner will now add or subtract two numbers instead of one. The third assignment follows the same pattern as the first two, focusing on two-digit multiplication and division.
Working Memory

In the VISUAL condition, the examiner exposes the numbers 4 2 1 in print; in the AUDITORY condition, the examiner says the numbers. Then, the participants will be asked to add 1 to each number the examiner shows or tells them. For example, when the examiner shows them 4 2 1 (VISUAL), handing the card to the students, they would be required to say 5 3 2.
In a different activity, the examiner would say three numbers, and the students would have to tell what the new numbers are and the examiner would experiment with various numbers. When instructed to add 1 to the displayed numbers, 2 4 7, the examiner would wait for a response from the student and ensure 3 5 8 be remembered by the student. If not, the examiner is required to correct them right away and walk the student through the process.













Leave feedback about this